円管内の流れ(ポアズイユ流れ)
一言で表すと、、
ポアズイユ流れとは、円管内を流れるニュートン流体の層流で、圧力勾配により流れが発生し、流速が管の中心で最大になる流れの状態を指します。
概要
ポアズイユ流れ(Poiseuille flow)は、円管内での流体の層流に関する理論的な流れのモデルです。
この流れは、ニュートン流体(粘性がある流体)が圧力勾配により流れるときの流速分布を示します。
ポアズイユ流れは、流体力学における基本的な概念であり、特に粘性流体の流れの解析や設計において重要です。
イメージ
ポアズイユ流れを理解するためには、以下のようなイメージを持つと良いでしょう。
- 流速の分布:
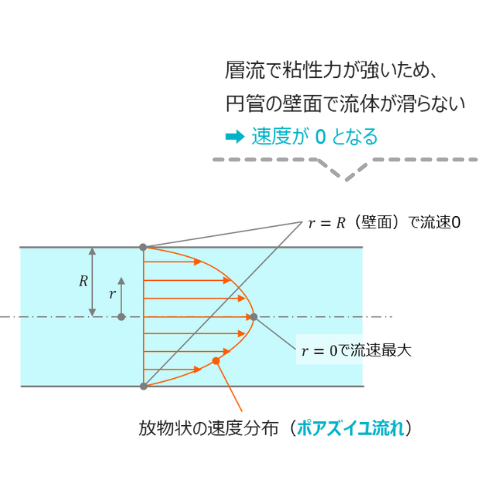
円管内の流れでは、流速が管の中心で最も速く、管壁に近づくにつれて徐々に遅くなることをイメージします。
これは、流体が管壁に接触する際に粘性抵抗が大きくなるためです。 - 圧力勾配:
圧力が管の一端からもう一端に向かって減少することで、流れが発生する様子を考えてください。
圧力差が流れを駆動します。
定義
ポアズイユ流れは、以下の条件の下で成立します:
- 円管内の層流: 流体が円管内を層流で流れる場合。
- ニュートン流体: 粘性がある流体で、せん断応力が流速の勾配に比例する場合。
- 圧力勾配: 圧力が円管内で均一に勾配があり、流れが発生する場合。
ポアズイユ流れの流速分布は次の式で表されます:
$$
v(r) = \frac{\Delta P}{4 \mu L} \left(R^2 – r^2\right)
$$
ここで、
- \( v(r) \) : 半径 \( r \) での流速(m/s)
- \( \Delta P \) : 管内の圧力差(Pa)
- \( \mu \) : 流体の動粘度(Pa·s)
- \( L \) : 管の長さ(m)
- \( R \) : 管の半径(m)
流量 \( Q \) は以下の式で求められます:
$$
Q = \frac{\pi R^4 \Delta P}{8 \mu L}
$$
CAEにおける重要性
CAE(Computer-Aided Engineering)では、ポアズイユ流れを用いて以下のような分析や設計が行われます。
- 流体の流れ解析: ポアズイユ流れのモデルを基に、円管内での流体の流れを解析し、流量や流速分布を予測します。
- 設計の最適化: 管の設計において、流体の流れの最適化や粘性抵抗の最小化を図るために、ポアズイユ流れの理論が利用されます。
物理的意味合い
ポアズイユ流れは、以下の物理的意味を持ちます。
- 層流の流速分布:
ポアズイユ流れは、円管内の層流における流速分布を示し、管の中心で最も速く、管壁に近づくにつれて流速が低下します。 - 圧力と粘性の影響:
流れの発生には圧力勾配が関与し、流体の粘性が流速分布に影響を与えます。
この関係を理解することで、流体の運動や抵抗を予測できます。
まとめ
ポアズイユ流れは、円管内でのニュートン流体の層流に関する基本的な理論であり、流速分布や流量の計算に利用されます。
流体の粘性や圧力勾配の影響を考慮した流れの解析は、CAE解析において重要です。
ポアズイユ流れを理解することで、流体の挙動を予測し、効率的な設計や解析を行うことができます。




コメント