各種管路形状における圧力損失の計算方法

配管設計において、圧力損失を正確に計算することは非常に重要です。
前回の記事では、圧力損失の基本的な概念から、直管部の圧力損失の計算方法までを詳しく解説しました。

圧力損失の計算と配管設計：ダルシー・ワイズバッハの式からレイノルズ数の計算まで

配管システムの圧力損失は流体のエネルギー損失を引き起こし、システムの効率やコストに影響します。この記事では、ダルシー・ワイズバッハの式からレイノルズ数の計算、層流と乱流の分類、管摩擦係数の求め方まで、配管設計に必要な知識を網羅しています。

ms-fan.com

しかし現実的には、圧力損失は配管内の流体が直線の管を流れる場合だけでなく、曲がり管、拡大管、分岐管、バルブなど、さまざまな要素によっても生じます。

本記事では、6種類の管路形状による圧力損失の計算方法について解説します。

管路形状による圧力損失の計算方法

急激に流路が縮小する場合

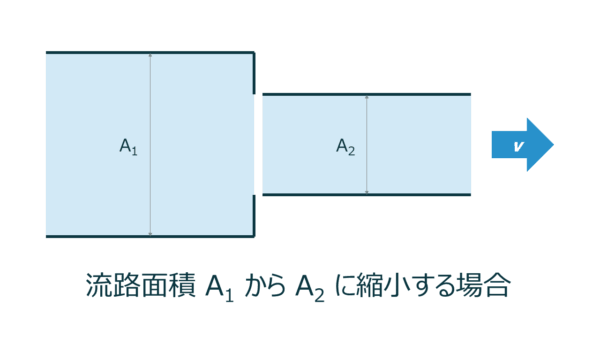
急激な縮小が発生すると、流れが乱流になり圧力損失が増加します。

縮小部での圧力損失は、損失係数 \( \zeta \) （ゼータ）を使って計算します。
計算式は以下の通りです。

$$
h = \zeta \times \left( \frac{v^2}{2g} \right)
$$

$$
\zeta = \left(\frac{1}{C} – 1\right)^2
$$

ここで、

• \( h \) ：圧力損失
• \( \zeta \) ：損失係数
• \( v \) ：流速
• \( g \) ：重力加速度

縮小係数 \( C \) は、流路面積の比率 \( \frac{A_2}{A_1} \) に応じて決定されます。
以下の表を参考にしてください。

\( \frac{A_2}{A_1} \)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
\( C \)	0.61	0.62	0.63	0.65	0.67	0.70	0.73	0.77	0.84

縮小する間に仕切りがある場合

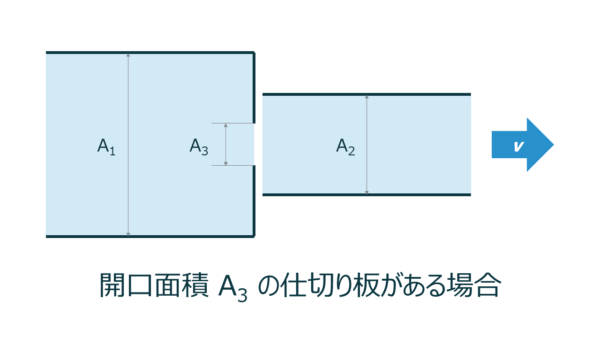
仕切りがある縮小部でも同様に損失係数 \( \zeta \) を用いますが、\( \frac{A_3}{A_1} \) の面積比に基づいて損失係数 \( \zeta \) は決定されます。

$$
h = \zeta \times \left( \frac{v^2}{2g} \right)
$$

$$
\zeta = 0.04 \left(\frac{A_2}{A_3}\right)^2 + \left(\frac{A_2}{C A_3} – 1\right)^2
$$

\( \frac{A_3}{A_1} \)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
\( \zeta \)	0.63	0.64	0.65	0.67	0.69	0.72	0.77	0.85	0.92

一方、\( \frac{A_3}{A_1} \) が10%以下の場合、次の表に基づいた損失係数 \( \zeta \) を使用します。

\( \frac{A_3}{A_2} \)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
\( \zeta \)	232	51	20	9.6	5.2	3.1	1.9	1.2	0.7	0.5

急激に流路が拡大する場合

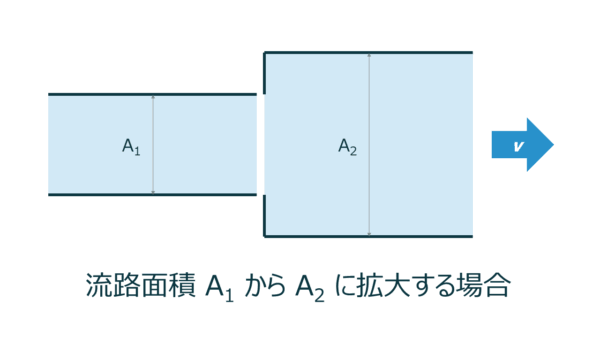
流路が急激に拡大する場合も圧力損失 \( \zeta \) が発生します。
これは流体が拡散することで流速が急激に減少し、エネルギーが損失するためです。

この場合の損失係数 \( \zeta \) は、拡大率に応じた値を使用して計算します。

$$
h = \zeta \times \left( \frac{v^2}{2g} \right)
$$

$$
\zeta = \left(1 – \frac{A_1}{A_2}\right)^2
$$

曲げ管（エルボ）の場合

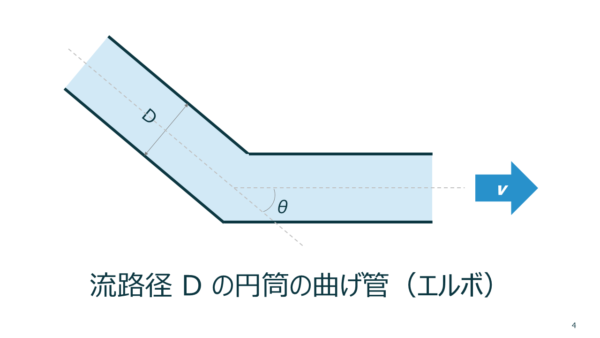
流路が直角やカーブで曲がるエルボでは、流体が方向を変えるためにエネルギーを失い、圧力損失 \( \zeta \) が発生します。

$$
h = \zeta \times \left( \frac{v^2}{2g} \right)
$$

$$
\zeta = 9.5 \left(\sin{\frac{\theta}{2}}\right)^2
$$

エルボの角度に応じて損失係数 \( \zeta \) が変わります。
以下の表を参照してください。

角度θ	20	40	60	80	90	100	110	120	130
\( \zeta \)	0.072	0.286	0.635	1.112	1.392	1.697	2.025	2.375	2.741

分岐管の場合

分岐管では、流れが分かれる場合（分流）と、流れが合流する場合（合流）で、圧力損失の計算方法が異なります。
また、主管側と支管側での損失係数が異なるため、それぞれの状況に応じた計算が必要です。

以下に、分岐管の圧力損失の計算法について詳しく説明します。

分流および合流における圧力損失の計算法

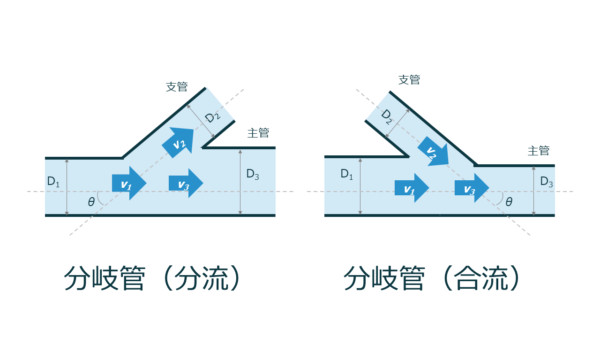
分岐管での圧力損失は流れ経路ごとに発生し、それぞれ損失係数 \( \zeta \) を使用して、圧力損失を計算します。

$$
h = \zeta \times \left( \frac{v^2}{2g} \right)
$$

ここで、

• \( h \) ：圧力損失
• \( \zeta \) ：損失係数
• \( v \) ：流速
• \( g \) ：重力加速度

具体的には、次のような流れ経路で損失係数を使用します。

状況	流れ経路	圧力損失
分岐流	主管（1→3）	\( h = \zeta_1 \times \left( \frac{v_1^2}{2g} \right) \)
分岐流	支管（1→2）	\( h = \zeta_2 \times \left( \frac{v_1^2}{2g} \right) \)
合流	主管（1→3）	h\( h = \zeta_1 \times \left( \frac{v_3^2}{2g} \right) \)
合流	支管（2→3）	h\( h = \zeta_2 \times \left( \frac{v_3^2}{2g} \right) \)

分岐管における損失係数 ζ の値

分岐管での損失係数 \( \zeta \) は、流量比や流路の面積比（ \( \frac{A_2}{A_1} \) ）に基づいて変化します。
具体的な数値は、以下の表を参照してください。

表では、分岐流（流量が分かれる場合）と合流（流量が合流する場合）における、流量の割合（管路2の流量/管路1の流量や管路2の流量/管路3の流量）に対する損失係数 \( \zeta_1 \) および \( \zeta_2 \) の値が記載されています。

【分岐流（流量が分かれる場合）】

A2/A1	θ	ζ	管路2の流量/管路1の流量
			0	0.2	0.4	0.6	0.8	1.0
1	90	\(\zeta_1\)	0.05	-0.08	-0.05	0.07	0.21	0.35
		\(\zeta_2\)	0.96	0.88	0.89	1.14	1.29	1.3
	45	\(\zeta_1\)	0.04	-0.07	-0.04	0.08	0.33	0.4
		\(\zeta_2\)	0.8	0.67	0.5	0.37	0.47	0.5
0.338	90	\(\zeta_1\)	0.2	-0.15	-0.05	0.2	0.3	0.35
		\(\zeta_2\)	1.3	1.5	2.35	4.3	5.0	7.0
	45	\(\zeta_1\)	0	-0.05	-0.03	0.07	0.35	0.4
		\(\zeta_2\)	0.92	0.75	0.5	3.3	5.3	7.2
0.122	90	\(\zeta_1\)	0	0	0	0	0	0
		\(\zeta_2\)	0.98	2.95	8.83	19.4	31.3	41.0
	45	\(\zeta_1\)	-0.01	0.01	0.21	0.34	0.5	0.6
		\(\zeta_2\)	1	1.0	6.0	14.0	27.0	30.0

【合流（流量が合流する場合）】

A2/A1	θ	ζ	管路2の流量/管路3の流量
			0	0.2	0.4	0.6	0.8	1.0
1	90	\(\zeta_1\)	0.35	0.04	0.18	0.3	0.4	0.5
		\(\zeta_2\)	-1.01	-0.41	0.08	0.46	0.72	0.9
	45	\(\zeta_1\)	0.33	0.04	0.17	0.18	0.06	-0.17
		\(\zeta_2\)	-0.91	-0.37	0	0.22	0.37	0.37
0.338	90	\(\zeta_1\)	0.54	0.77	0.1	1.25	1.5	1.75
		\(\zeta_2\)	-0.7	0.2	1.25	2.8	4.78	7.25
	45	\(\zeta_1\)	0.1	-0.2	-0.7	-1.5	-2.89	-3.6
		\(\zeta_2\)	-1	-0.1	0.75	2.1	3.7	5.53
0.122	90	\(\zeta_1\)	0	0	0	0	0	0
		\(\zeta_2\)	-1.18	2.34	11.6	29.1	38.2	45.3
	45	\(\zeta_1\)	-0.01	-1.1	-2.9	-5.7	-7.8	-9.62
		\(\zeta_2\)	1	1.0	6	14	27	44.5

損失係数 \( \zeta \) は、流路の形状や角度、流量比によって大きく変動するため、正確な計算が必要です。

これにより、分岐管における全体的な圧力損失を正確に予測することができます。

弁などの調節機器

弁（バルブ）は、配管システムにおいて流量を調整する重要な機器です。

弁が設置されると、流体の流れが変化し、圧力損失が発生します。
弁の種類や大きさにより、この圧力損失の大きさは異なります。

ここでは、代表的な弁の圧力損失について、相当長さを用いた計算方法を解説します。

弁の圧力損失の計算

弁が配管に挿入された場合、その弁の圧力損失は、管路の直管部の長さに換算することが一般的です。
これを「相当長さ（ \( L_e \) ）」と呼びます。

相当長さを用いて圧力損失を計算する場合、ダルシー・ワイズバッハの式を用います。

$$
h_f = f \times \left(\frac{L_e}{D}\right) \times \left(\frac{v^2}{2g}\right)
$$

ここで、

• \( h_f \) ：摩擦による圧力損失
• \( f \) ：摩擦係数
• \( L_e \) ：弁の相当長さ
• \( D \) ：配管の直径
• \( v \) ：流速
• \( g \) ：重力加速度

各種弁の相当長さLeの値

以下の表に、代表的な3種類の弁について、管径ごとの相当長さ \( L_e \) の値を示します。

これらの値を使用して、実際の配管設計における圧力損失を計算します。

管径 (inch)	仕切弁（ゲート弁）	玉形弁（グローブ弁）	アングル弁
1/2	0.01	3.25	1.63
3/4	0.17	4.49	2.3
1	0.23	6.88	3.56
1 1/4	0.3	8.38	4.02
1 1/2	0.37	10.2	5.08
2	0.63	13.8	6.89
2 1/2	0.77	21.1	8.69
3	0.88	24.8	10.5
3 1/2	1.07	28.5	14.3
4	1.31	36.3	18.1
5	1.61	43.9	22.9
6	2.21	59.5	29.5
8	2.79	74.4	37.2
10	3.35	89.3	44.5
12	3.35	89.3	44.5

各種弁の説明と圧力損失の特性は以下の通りです。

• 仕切弁（ゲート弁）：全開時に最も圧力損失が少ない弁です。弁内部に流路の変化が少ないため、相当長さも小さくなります。
• 玉形弁（グローブ弁）：流路が大きく曲がる構造をしているため、圧力損失が大きくなります。相当長さも仕切弁に比べて大きく、圧力損失が発生しやすい弁の一つです。
• アングル弁：直角に流れを変える構造を持つため、圧力損失は中程度ですが、グローブ弁よりは低い圧力損失を示します。

調節弁の圧力損失

調節を行う弁（例：バタフライ弁やスロットル弁）は、弁開度に応じて圧力損失が可変となります。

このため、調節弁における圧力損失を厳密に計算することは難しいですが、一般的には全圧力損失の40%〜50%を想定して設計することが推奨されます。

圧力損失の合計と計算方法のまとめ

設計者は、各配管や機器における圧力損失を見積もり、システム全体として十分な流体力学的性能を発揮できるようにすることが求められます。

圧力損失の合計

全体の圧力損失 \( h_{\text{total}} \)​ は、次のように各部の圧力損失の合計として計算されます。

$$
h_{\text{total}} = h_{\text{直管部}} + h_{\text{曲げ管}} + h_{\text{拡大縮小}} + h_{\text{合流分岐}} + h_{\text{バルブや機器}}
$$

• \( h_{\text{直管部}} \) ​：式 (1) 〜 (5) で計算される直管部分の圧力損失。
• \( h_{\text{曲げ管}} \) ​：曲がり配管（エルボなど）による圧力損失。
• \( h_{\text{拡大縮小}} \) ​：管径の急激な拡大・縮小による圧力損失。
• \( h_{\text{合流分岐}} \) ​：分岐や合流による圧力損失（分岐管やティー管）。
• \( h_{\text{バルブや機器}} \) ​：弁や機器の相当長さを基にした圧力損失。

圧力損失の導出例

例えば、あるシステムに以下の要素が含まれているとします。

1. 直管部（100m）
2. エルボ（90°が2つ）
3. 縮小管
4. 分岐管
5. グローブ弁

この場合、以下の手順で圧力損失を求めます。

1. 直管部の圧力損失は、ダルシー・ワイズバッハの式を使って計算します。

$$
h_{\text{直管部}} = f \times \frac{L}{D} \times \frac{v^2}{2g}
$$

2. 曲げ管（エルボ）による圧力損失は、損失係数 \( \zeta \) を使用して計算します。
   エルボの角度と個数に応じた損失係数を使用します。

$$
h_{\text{曲げ管}} = \zeta \times \frac{v^2}{2g}
$$​

3. 縮小管の圧力損失は、縮小係数 \( C \) を用いた式で算出します。

$$
h_{\text{縮小}} = C \times \frac{v^2}{2g}
$$

4. 分岐管の圧力損失は、分岐流と合流流における損失係数 \( \zeta \) を参照して計算します。
   
5. グローブ弁の圧力損失は、相当長さ \( L_e \)​ を直管の長さに換算して計算します。

$$
h_{\text{グローブ弁}} = f \times \frac{L_e}{D} \times \frac{v^2}{2g}
$$​

圧力損失を最適化するためのポイント

• 配管の直径選定：流体の流速が速すぎると圧力損失が増加するため、適切な直径を選定することが重要です。
• 流れのスムーズ化：曲げ管や縮小部をできるだけ少なくし、流れをスムーズにすることで、圧力損失を最小限に抑えます。
• 機器の配置：バルブやフィルターなどの機器を最小限に配置し、相当長さを短くすることも圧力損失を抑えるポイントです。

まとめ

配管システムにおける圧力損失の計算は、システム全体の性能を決定する上で非常に重要なステップです。

流体が直管を通過する場合の圧力損失に加え、曲がり管、拡大・縮小管、分岐管、バルブや機器などの各要素でも圧力損失が生じます。

それぞれの要素で発生する圧力損失は、損失係数 \( \zeta \) を使用して正確に見積もることができます。

今回の記事では、以下の要素について詳細に説明しました：

1. 急激な流路の縮小：縮小係数 \( C \) を用いて計算する方法。
2. 流路内に仕切りがある場合：流路面積比に基づいた損失係数の算出。
3. 急激な流路の拡大：流速と面積比から損失を求める方法。
4. 曲げ管：エルボなどの角度による圧力損失。
5. 分岐管：分岐および合流における圧力損失の計算。
6. バルブや調節機器：弁の種類や相当長さによる圧力損失の推定。

これらの要素の圧力損失をすべて合計することで、配管システム全体の圧力損失を算出することができます。
これにより、配管設計において適切な流量やポンプの選定を行うことが可能です。

設計者へのポイント

• 損失を最小限に抑える：曲げや分岐、縮小部分が多い配管では圧力損失が大きくなるため、できるだけ直線的な配管配置を心がけることが理想的です。
• 正確な計算：各要素の損失係数を適切に選定し、計算の精度を高めることが、システム全体の効率を向上させる鍵です。
• 全体的な見直し：各部分の圧力損失を詳細に検討し、必要に応じて配管サイズやバルブの選定を見直すことで、最適なシステム設計が可能となります。

今後、設計において圧力損失を正確に計算するために、この記事で紹介した計算式や損失係数を参考にしていただければと思います。
圧力損失の管理は、エネルギー効率やメンテナンスコストの低減にも繋がる重要な要素です。