平行壁間の流れ
一言で表すと、、
平行壁間の流れとは、ポアズイユ流れとクェット流れが組み合わさった流れのことで、狭い隙間を持つ平行な壁間での流体の流れを示します。
概要
平行壁間の流れは、ポアズイユ流れとクェット流れが融合した状態を示します。
ポアズイユ流れは圧力勾配により流体が流れる場合に、クェット流れは平板の動きによって流体が流れる場合の流れです。これらが平行な壁間でどのように組み合わさるかを理解することで、流体の複雑な挙動をより正確に解析できます。
イメージ
平行壁間の流れを理解するためには、以下のイメージを持つと良いでしょう:
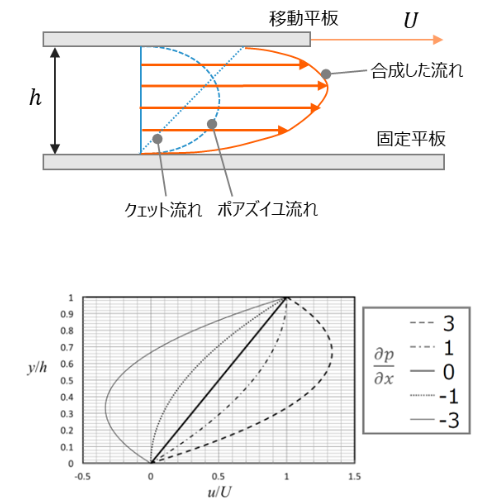
- ポアズイユ流れ: 流体が圧力勾配によって一方向に流れる状態。管内の流れや圧力差による流れが該当します。
- クェット流れ: 片方の平板が一定速度で平行に移動し、流体がせん断応力によって流れる状態。
- 組み合わせた流れ: 平行な壁間で、圧力勾配と平板の動きによるせん断流れが同時に作用し、複合的な流れが形成されます。
定義
平行壁間の流れは、次の条件を満たす流れを指します:
- ポアズイユ流れとクェット流れの和: 平行な壁間で、圧力勾配と平板の動きによるせん断流れが同時に作用する流れ。
- 定常流れ: 流れが時間とともに変化せず、一定の状態を保っていること。
- 線形速度分布: 流体の速度が位置によって線形に変化し、圧力勾配とせん断応力の両方の影響を受ける。
ポアズイユ流れとクェット流れの組み合わせにより、以下のような速度分布が得られます:
$$
v(y) = \frac{U}{h} \cdot y + \frac{P}{4 \mu} \cdot (h^2 – y^2)
$$
ここで、
- \( v(y) \) : 位置 \( y \) での流体の速度(m/s)
- \( U \) : 移動平板の速度(m/s)
- \( P \) : 圧力差(Pa)
- \( \mu \) : 流体の動粘度(Pa·s)
- \( h \) : 平板間の距離(m)
CAEにおける重要性
CAE(Computer-Aided Engineering)において、平行壁間の流れは以下のようなケースで重要です:
- 複合流れのシミュレーション: ポアズイユ流れとクェット流れの組み合わせによる複合的な流れをシミュレーションし、現実の流体システムにおける挙動を予測します。
- 流体システムの設計: 平行壁間の流れを考慮して、効率的な設計や最適化を行い、圧力損失やエネルギー損失を最小化します。
物理的意味合い
平行壁間の流れの物理的意味合いは以下の通りです:
- 圧力勾配とせん断応力の組み合わせ: 流れは圧力勾配とせん断応力の両方の影響を受け、複雑な速度分布を形成します。
- 流体挙動の複合性: ポアズイユ流れとクェット流れの和により、流体の挙動がより複雑になり、流体力学的な解析が重要となります。
まとめ
平行壁間の流れは、ポアズイユ流れとクェット流れが組み合わさった状態を示します。この流れの理解は、複合的な流体システムの設計や解析において重要です。CAE解析においても、平行壁間の流れを考慮することで、より正確なシミュレーションが可能となり、設計の最適化や性能向上に役立ちます。




コメント