一言で表すと、、
ニュートンの粘性法則とは、流体のせん断応力が流速の勾配に比例することを示す法則で、流体の粘性を定量化するための基本的な理論です。
概要
ニュートンの粘性法則(Newton’s law of viscosity)は、流体が流れるときに生じるせん断応力と流速勾配との関係を示します。この法則は、流体の粘性(内部摩擦)を理解し、流体の動きを予測するための基本的な理論です。
ニュートンの粘性法則は、ニュートン流体に適用され、流体力学のさまざまな分野で利用されています。
イメージ
ニュートンの粘性法則を理解するためには、以下のようなイメージを持つと良いでしょう。
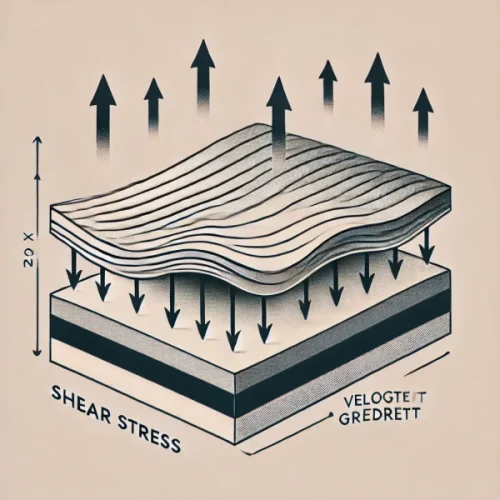
- 流体のせん断応力: 流体が層状に流れるとき、異なる層間での速度差によってせん断応力が発生します。せん断応力は、速度の勾配に応じて変化します。
- 粘性の影響: 粘性のある流体は、流速が大きいほどせん断応力が大きくなります。これにより、流体の動きが抵抗されることをイメージできます。
定義
ニュートンの粘性法則は、以下の式で定義されます:
$$
\tau = \mu \frac{du}{dy}
$$
ここで、
- \( \tau \) はせん断応力(Pa)
- \( \mu \) は動粘度(Pa·s)
- \( \frac{du}{dy} \) は流速勾配(1/s)
この式は、流体がせん断応力に応じてどのように流れるかを示しており、流速の勾配に比例したせん断応力が発生します。
ニュートン流体では、せん断応力と流速勾配の関係が線形であり、粘度は一定とされます。
CAEにおける重要性
CAE(Computer-Aided Engineering)では、ニュートンの粘性法則を用いて以下のような解析が行われます。
- 流体の挙動予測: ニュートンの粘性法則を基に、流体の流れやせん断応力を予測し、設計やシミュレーションに活用します。
- 構造解析: 流体の粘性による影響を考慮して、構造物の耐久性や性能を評価します。特に、流体と構造物の相互作用を解析する際に重要です。
物理的意味合い
ニュートンの粘性法則は、以下の物理的意味を持ちます。
- せん断応力と流速勾配の関係: 粘性流体において、せん断応力は流速勾配に比例し、粘度によってその関係が定量化されます。この関係により、流体の挙動を正確に予測できます。
- ニュートン流体の特徴: ニュートン流体では、せん断応力と流速勾配の関係が線形であり、粘度が一定とされます。これにより、流体の粘性の影響を簡単にモデル化できます。
まとめ
ニュートンの粘性法則は、流体のせん断応力と流速勾配との関係を示す基本的な理論であり、流体の粘性を定量化するために重要です。
CAE解析においては、ニュートンの粘性法則を用いて流体の挙動を予測し、設計やシミュレーションに役立てることができます。流体の粘性を理解することで、より正確な解析と効果的な設計が可能になります。



コメント