サマリ
今回は、衝撃波の可視化に利用されるシュリーレン法とシャドウグラフ法という2つの光学的可視化技術についてご紹介します。
これらの手法を用いることで、気体や液体の密度変化を目に見える形で捉えることができます。
詳細
シュリーレン法とシャドウグラフ法は、気体や液体の密度変化を可視化するための技術で、どちらも光の屈折現象を利用しています。
光が異なる密度の媒質を斜めに通過すると、屈折が発生します。この屈折は、スネルの法則に従い、光の入射角と屈折角が媒質の屈折率に依存して決まります。
気体中での屈折率は、Gladstone-Daleの関係式に基づいて密度に比例して変化します。
Gladstone-Daleの関係式
$$
n = k \rho +1
$$
屈折率と密度の関係は、Gladstone-Dale定数 \( k \) を用いて表されます。
これは気体の種類によって決まる定数で、通常、1E-4~1.5E-3の範囲にあります。
しかし、気体の屈折率は非常に小さな変化しか示さないため、この変化を可視化するには特別な光学技術が必要です。
シュリーレン法とシャドウグラフ法は、こうした微小な屈折率の差を、明暗のコントラストとして捉えることができる手法です。
手法の特徴
- シュリーレン法:密度の一次微分に敏感で、急激な密度変化を明瞭に捉えます。
- シャドウグラフ法:密度の二次微分に敏感で、細かな密度変化を捉えるのに適しています。
それぞれの方法を用いて、斜め衝撃波を可視化する具体例を見てみましょう。
解析事例:斜め衝撃波
ここでは、デルタ翼がマッハ2.0で飛行している状況を模擬し、衝撃波を可視化します。
条件は、高度 0.0 [m]、温度 288 [K]、デルタ翼の幅 0.06 [m]で設定しています。
この条件下でのレイノルズ数 \( \text{Re} \) は約 2.7E+6 です。
翼表面には断熱壁条件を適用し、外部流れ場には自由流れ境界を設定しています。
シュリーレン法
シュリーレン法での可視化を行うにあたって、以下の式を用います。
$$
NS = c_{1} exp \left[ \frac{- c_{2} (\vert \nabla \rho \vert – \vert \nabla \rho \vert _{min} )}{(\vert \nabla \rho \vert _{max} – \vert \nabla \rho \vert _{min} )} \right]
$$
ここで、\( c_1 \) と \( c_2 \) は定数です。今回はそれぞれ0.8と1000で設定します。
シュリーレン法を用いて可視化を行う際には、以下の手順を踏みます。
- フィールド関数の作成:密度の勾配( \( \nabla \rho \) )の絶対値を計算し、フィールド関数として用意します。
- レポートの作成:密度勾配の最小値と最大値( \( \nabla \rho _{min} \) と \( \nabla \rho _{max} \) )を求めるためのレポートを作成します。
- フィールド関数の作成(Schlieren):上記で得られたデータを元に、Numerical Schlierenフィールド関数を定義します。
- シーンの作成:スカラーシーンを作成し、必要な部分が見えるように設定します。
- 背景:黒
- カラーバー:グレースケール
- 反転:On
- フィールド関数:Schlieren

シャドウグラフ法
シャドウグラフ法を使用する際には、密度のラプラシアンを計算する必要があります。以下の手順で進めます。
- フィールド関数の作成:密度のラプラシアンを計算し、「Shadowgraph」という名前で保存します。
- シーンの作成:スカラーシーンを作成し、見たい部分が明確になるように設定します。
- 背景:黒
- カラーバー:グレースケール
- 反転:On
- フィールド関数:Shadowgraph
- 値の範囲:±1E-04 に設定
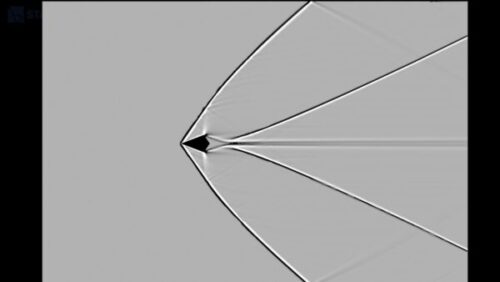
これらの手法を使って生成された画像を見ると、デルタ翼の先端から斜めに伸びる衝撃波が確認できます。
また、デルタ翼の後方では、密度変化が明確に見られ、乱流と膨張波の相互作用が起きていることがわかります。
まとめ
シュリーレン法とシャドウグラフ法は、気体や液体の密度変化を視覚化するための強力な手法です。それぞれの方法は異なる特性を持ち、特定の状況下で効果的に使用できます。
シュリーレン法は急激な密度変化を捉えるのに適しており、シャドウグラフ法は細かい密度変化を明確に表現します。これらの技術を駆使することで、流体力学や衝撃波の研究において非常に有益な情報を得ることが可能です。





コメント