レイノルズ数
一言で表すと、、
レイノルズ数とは、流体の流れの性質を示す無次元数で、流れの層流から乱流への遷移を判断するための指標です。
概要
レイノルズ数は、流体力学における基本的な無次元数で、流体の流れが層流か乱流かを判断するために使用されます。
この数値は、流体の速度、密度、粘度、そして物体の特性などに依存し、流れの安定性や乱れ具合を示します。
レイノルズ数が高いほど、流れは乱流に近く、低いほど層流に近いとされます。
イメージ
レイノルズ数を理解するためには、以下のようなイメージを持つと良いでしょう。
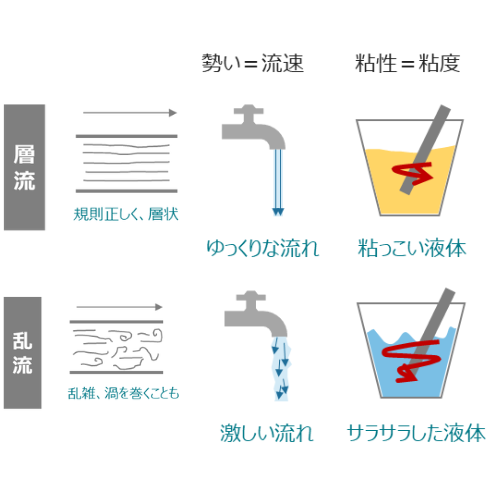
- 層流と乱流: 流れが規則正しく平行に進む層流と、複雑で乱れた流れの乱流を比較する際、レイノルズ数がその区別に役立ちます。
例えば、ゆっくりと流れる水の中での層流と、速く流れる水の中での乱流を考えたとき、レイノルズ数がその流れのタイプを示します。 - 速度と粘度の関係: 高速で流れる流体や粘度が低い流体では、レイノルズ数が高くなる傾向があります。
この場合、流れは乱流になる可能性が高いです。
定義
レイノルズ数(Re)は、以下の式で定義されます:
$$
\text{Re} = \frac{\rho v L}{\mu}
$$
ここで、
- \( \rho \) : 流体の密度(kg/m³)
- \( v \) : 流体の流速(m/s)
- \( L \) : 流れの特性長さ(m)
- \( \mu \) : 流体の動粘度(Pa·s)
レイノルズ数は無次元であり、流れの状態を表すために用いられます。具体的には、レイノルズ数が次のように分類されます:
- 層流 : レイノルズ数が小さい場合、流れは層流であり、流体の層が平行に流れます。
- 遷移領域 : レイノルズ数が中程度の範囲では、流れが層流から乱流に遷移する過渡状態です。
- 乱流 : レイノルズ数が大きい場合、流れは乱流であり、流体の運動が不規則で混沌としています。
CAEにおける重要性
CAE(Computer-Aided Engineering)では、レイノルズ数を利用して流体の流れの特性を予測し、解析を行います。具体的には、以下のような点で重要です。
- 流れのモデル化: レイノルズ数を使用して、実際の流れの層流から乱流までの状態をモデル化し、シミュレーションの精度を向上させます。
- 設計の最適化: 工業設計や製品開発において、レイノルズ数を基に流体の流れを最適化し、効率的な設計を実現します。
物理的意味合い
レイノルズ数は、流体力学における以下のような物理的意味を持ちます。
- 流れの性質 : レイノルズ数が高いと流れは乱流になり、低いと層流になるという流体の運動状態を示します。
- スケール依存性 : レイノルズ数は流体のスケールや条件に依存するため、異なる条件下での流れの挙動を比較するために重要です。
まとめ
レイノルズ数は、流体の流れが層流から乱流へと遷移する際の重要な指標です。
流体の速度、密度、粘度、特性長さに基づき、流れの性質を無次元で示します。
CAE解析においては、レイノルズ数を利用して流れのモデル化や設計の最適化を行い、精度の高いシミュレーションを実現します。
レイノルズ数の理解は、流体力学の問題解決において非常に重要です。



コメント