永田の式と邪魔板なし条件での撹拌動力推算を詳しく解説

コンテンツ

邪魔板なし条件での撹拌動力推算（永田の式）
まとめ

邪魔板なし条件での撹拌動力推算（永田の式）

一言で表すと、、

邪魔板（バッフル）なしの条件下での撹拌動力を推算するには、レイノルズ数と動力数の関係を考慮した永田の式が有効です。

これは特に高レイノルズ数領域で動力数が減少する傾向を説明します。

概要

撹拌プロセスにおいて、邪魔板なし条件はシンプルな構造であり、撹拌効率に影響を与える要因が少ない環境です。

邪魔板を用いない場合、撹拌効率の向上を図るために、レイノルズ数（Re）に基づいた動力推算が重要となります。

特に高レイノルズ数領域では、流体が乱流状態になり、動力数（Np）が減少する傾向にあります。

撹拌翼としてパドル翼を使用する場合、永田の式が代表的な動力推算式として活用されます。
これは、撹拌翼の幅と液深さの比率に基づき、正確な動力計算を行うための式です。

イメージ

邪魔板を使わない撹拌槽をイメージしてください。

この条件下では、流体は撹拌翼の回転により混合されますが、流れが容器内で乱流を引き起こしやすくなります。
邪魔板がないため、流体の自然な流れが強調され、動力数がレイノルズ数の増加に伴い低下します。

この現象を計算に取り込むのが、永田の式です。

定義

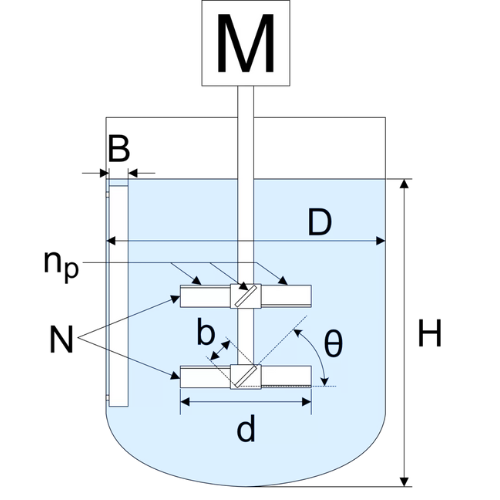
永田の式は、以下のように定義されます。

$$
N_P = \frac{A}{Re} + B \left( \frac{10^3 + 1.2Re^{0.66}}{10^3 + 3.2Re^{0.66}} \right)^p \left( \frac{H}{D} \right)^{(0.35 + b/D)}
$$

$$
A = 14 + \frac{b}{D} \left( 670 \left( \frac{d}{D} – 0.6 \right)^2 + 185 \right)
$$

$$
B = 10^{{ 1.3 – 4(b/D – 0.5)^2 – 1.14(d/D) }}
$$

$$
p = 1.1 + 4 \left( \frac{b}{D} \right) + 2.5 \left( \frac{d}{D} – 0.5 \right)^2 – 7 \left( \frac{b}{D} \right)^4
$$

ここで、

$ Np $ : 動力数（無次元）
$ Re $ : レイノルズ数（無次元）
$ H $ : 液深さ（m）
$ D $ : 撹拌槽の直径（m）
$ b $ : 撹拌翼の幅（m）
$ d $ : 撹拌翼の直径（m）

永田の式は、特に邪魔板なし条件での動力推算に適しており、レイノルズ数の増加に伴い、動力数（ $ N_p $ ）が減少することを示しています。
これにより、邪魔板を使用しない場合の撹拌効率を評価できます。

高レイノルズ数領域では、乱流が強くなるため、動力数の低下は顕著です。

撹拌翼が発生させる流れが広がることで、同じ回転速度でもより少ない動力で流体が撹拌されるため、動力効率が向上します。

また、永田の式はパドル翼を前提としています。

この式は、翼幅と液深さの比率（b’/H）が1を超えない範囲で有効に利用できます。

パドル翼条件の修正

永田の式は標準的な2枚羽根1段のパドル翼を前提としていますが、羽根の枚数や段数が異なる場合は、修正が必要です。

修正されたパドル翼条件は、以下のように表されます。

$$
b’ = \frac{n_p}{2} \times b \times N
$$

$ b’ $ : 修正後の翼幅（m）
$ n_p $ : 撹拌翼の枚数（無次元）
$ b $ : 翼幅（m）
$ N $ : 翼の段数（無次元）

この式により、複数段の撹拌翼や異なる羽根枚数の条件でも、永田の式を活用して正確な動力推算が行えます。

CAEにおける重要性

永田の式は、CAE解析においても有用です。
特に、邪魔板なし条件での撹拌動力の推算を行う際、数値流体力学（CFD）解析を用いて撹拌プロセスのシミュレーションが行えます。

CFD解析では、流体の動きや乱流の発生状況を視覚化し、永田の式に基づいた動力推算結果を確認できます。

これにより、工業規模での撹拌効率を最大化し、エネルギー消費を削減することが可能です。

物理的意味合い

邪魔板なし条件での撹拌における物理的意味合いは、以下の通りです。

動力数の減少: レイノルズ数が高いほど、撹拌時の乱流が強まり、動力数が減少します。このため、効率的な撹拌が可能になります。
乱流の発生: 邪魔板がないことで流れが自由に発生しやすくなり、乱流が支配的な流れになります。これにより、効率的な混合が可能になりますが、過剰な回転数はエネルギーの浪費につながる可能性もあります。
撹拌装置の設計最適化: 永田の式に基づいて動力推算を行うことで、最適な撹拌装置の設計が可能となり、撹拌効率とコストのバランスを取ることができます。

まとめ

永田の式を用いた邪魔板なし条件での撹拌動力推算は、撹拌プロセスにおいて非常に重要な役割を果たします。特に、高レイノルズ数領域での動力数の減少を考慮することで、効率的な撹拌を実現できます。

また、撹拌翼の形状や枚数、段数に応じた修正を行うことで、実際の装置設計に応じた正確な動力計算が可能となります。CAE解析やCFDを活用すれば、動力数のシミュレーションを行い、撹拌効率を最大限に引き出すことができます。

永田の式を理解し、適切に活用することで、撹拌装置の最適化とエネルギーコストの削減が期待でき、工業撹拌におけるプロセス改善に大きく貢献します。

邪魔板なし条件での撹拌動力推算（永田の式）を詳しく解説