動力数とレイノルズ数の関係
一言で表すと、、
動力数(Np)とレイノルズ数(Re)は、撹拌プロセスの効率と流体の流れの状態を評価するための無次元数であり、両者の関係を示す「Np-Re曲線」が撹拌効率の最適化に重要な役割を果たします。
概要
動力数( \( Np \) )とレイノルズ数( \( Re \) )は、流体の撹拌過程を評価する上で非常に重要な無次元数です。特に、撹拌効率を最大化するためには、これら二つの数値がどのように関連しているかを理解することが必要です。
- 動力数( \( Np \) )は、撹拌装置に供給される動力と流体の特性(密度や粘度など)との関係を示します。
- レイノルズ数( \( Re \) )は、流体の慣性力と粘性力の比率を表し、流体が層流か乱流かを判断する基準となる数値です。
動力数とレイノルズ数の関係は、「Np-Re曲線」と呼ばれるグラフで視覚的に示され、流れの状態に応じた撹拌効率を評価する際に使われます。
この曲線を理解することで、撹拌装置の運転条件を最適化することが可能となります。
イメージ
撹拌プロセスにおいて、レイノルズ数は流体の状態を、動力数は撹拌に必要なエネルギーの効率を示すと考えると理解しやすいです。
- レイノルズ数が低い( \( Re \) < 10)場合、流体は層流(穏やかな流れ)になり、撹拌に必要なエネルギーは少ないが、混合効率も低くなります。
- レイノルズ数が高い( \( Re \) > 10,000)場合、流体は乱流(激しい流れ)となり、撹拌は強力で効率的に行われますが、より多くのエネルギーが必要です。
「Np-Re曲線」を使うことで、流体がどのような状態で動力効率が最大になるかを視覚的に確認できます。
定義
動力数( \( N_p \) )の定義
動力数は次のように定義されます:
$$
N_p = \frac{P}{\rho \times N^3 \times D^5}
$$
- \( N_p \) :動力数
- \( P \) :撹拌機に供給される動力
- \( \rho \) :流体の密度
- \( N \) :撹拌機の回転数
- \( D \) :撹拌翼の直径
この式は、撹拌機の設計や運転効率を評価する際に重要な数値を提供します。
レイノルズ数( \( Re \) )の定義
レイノルズ数は次の式で表されます:
$$
Re=ρ×N×D2μRe = \frac{\rho \times N \times D^2}{\mu}
$$
- \( Re \) :レイノルズ数
- \( \rho \) :流体の密度
- \( N \) :撹拌機の回転数
- \( D \) :撹拌翼の直径
- \( \mu \) :流体の粘度
レイノルズ数は、流体の慣性力と粘性力のバランスを示し、流体が層流か乱流かを決定する要因です。
Np-Re曲線
「Np-Re曲線」は、動力数(Np)とレイノルズ数(Re)の関係を示すグラフであり、撹拌機の設計や運転条件の最適化に広く使用されます。
この曲線は、レイノルズ数の増加に伴って動力数がどのように変化するかを示します。
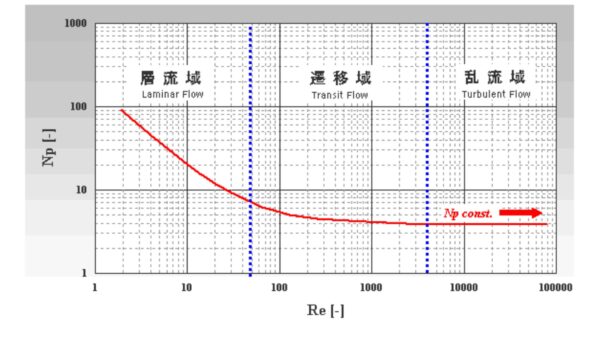
Np-Re曲線の特徴
- 層流領域(Re < 10)
この領域では、流体の動きは滑らかであり、撹拌に大きなエネルギーは必要とされません。
動力数(Np)はレイノルズ数に比例して減少します。
→ \( N_p ∝ Re^(-1) \) - 遷移領域(10 < Re < 10,000)
この範囲では、層流から乱流への移行が起こり、撹拌効率が向上しますが、同時にエネルギーの消費も増加します。この領域では、動力数は徐々に減少していきます。 - 乱流領域(Re > 10,000)
レイノルズ数が非常に大きくなると、流体は完全な乱流状態に入り、動力数はほぼ一定になります。この段階では、流れの抵抗が少なくなり、エネルギー効率は最高に達します。
→ \( N_p = \text{一定値} \)
Np-Re曲線の重要性
- 層流領域での動力数の最適化:エネルギー消費を抑えつつ、撹拌が効果的に行われるポイントを探すことが重要です。
- 乱流領域での動力数の安定化:乱流状態では撹拌効率が最大化されるため、エネルギーと撹拌効率のバランスを最適化するための基準になります。
CAEにおける重要性
CAE(コンピュータ支援工学)は、動力数とレイノルズ数の関係をシミュレーションし、撹拌機の設計に役立てるツールです。特に、Np-Re曲線を用いた解析により、撹拌効率の最適化が可能になります。
- 設計の最適化:CAEソフトウェアを用いて、撹拌機の設計や操作条件に応じた動力数とレイノルズ数の関係を詳細にシミュレーションできます。
- エネルギー効率の向上:Np-Re曲線を使って、撹拌プロセスのエネルギー消費を最小限に抑える条件を見つけることが可能です。
CAEを使用することで、撹拌効率を向上させつつ、エネルギーコストの削減も実現できます。
物理的意味合い
動力数とレイノルズ数の関係は、流体力学的な現象を理解するために重要です。
撹拌装置におけるエネルギーの供給や流体の動きを解析する際、この2つの無次元数がどのように相互作用するかを把握することが、効率的な撹拌設計に不可欠です。
- エネルギー消費と流れの状態:層流、遷移、乱流それぞれの領域で、撹拌に必要なエネルギーとその効率が異なります。レイノルズ数が増加するにつれて流体の乱れが大きくなり、撹拌がより効果的になる一方で、エネルギー消費も増加します。
- 撹拌効率:乱流領域では、エネルギー供給がほぼ一定で、撹拌効率は最大限に発揮されますが、効率化のためにはCAEやNp-Re曲線を用いて正確な設計が必要です。
まとめ
動力数( \( N_p \) )とレイノルズ数( \( Re \) )の関係は、撹拌装置の設計と効率を評価する上で非常に重要です。特に、Np-Re曲線は、流体の流れが層流から乱流へと変化する際に、撹拌効率がどのように変わるかを示すため、撹拌プロセスの最適化に不可欠なツールです。
CAEを活用することで、Np-Re曲線を基にした最適な撹拌機の設計が可能となり、エネルギーコストの削減やプロセス効率の向上を実現します。
撹拌プロセスの効率化に向けて、動力数とレイノルズ数の関係を正しく理解し、設計に反映させることが重要です。





コメント