ムーディ線図
一言で表すと、、
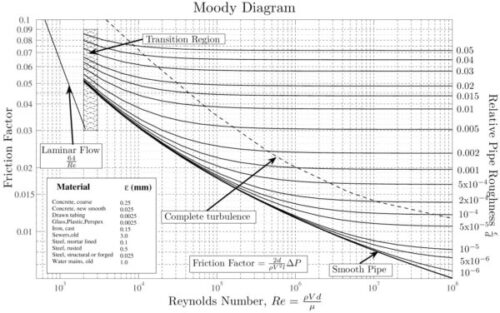
「ムーディ線図」とは、管内流れにおける摩擦係数をレイノルズ数と相対粗さの関係で可視化した図です。
流体の圧力損失計算に広く利用されます。
概要
ムーディ線図は、1944年にルイス・ムーディ(Lewis Moody)によって発表された図で、流体力学における圧力損失や摩擦係数の計算に欠かせないツールです。
この図は、管内の流体流れが層流から乱流にわたる全領域での摩擦損失を視覚化しており、流体がどのように流れ、どの程度のエネルギー損失が生じるかを定量的に評価することができます。
この線図では、縦軸に摩擦係数(\( f \) )、横軸にレイノルズ数(\( Re \) )がプロットされ、さらに相対粗さ(管の粗さ \( varepsilon \) を管径 \( D \) で割ったもの)がグラフ上に追加されています。
ムーディ線図は、工学や流体力学の設計プロセスで多用され、特に圧力損失を計算する場面で非常に重要です。
イメージ
ムーディ線図をイメージするには、次のようなシナリオを考えましょう。
例えば、あなたが水道管や石油パイプラインのような管内で流れる流体のエネルギー損失を予測しようとしています。
管が滑らかであればエネルギー損失は少なく、粗い場合には摩擦が増え、損失が大きくなります。
ムーディ線図は、この流体の挙動を簡単に把握するためのグラフです。
定義
ムーディ線図は、ダルシー・ワイスバッハの式を基にした摩擦係数の視覚化ツールです。
ダルシー・ワイスバッハの式は次のように表されます。
$$
h_f = f \frac{L}{D} \frac{V^2}{2g}
$$
- \( h_f \) : 圧力損失(高さに換算)
- \( f \) : ダルシー摩擦係数(ムーディ線図で得られる値)
- \( L \) : 管の長さ
- \( D \) : 管の直径
- \( V \) : 流体の速度
- \( g \) : 重力加速度
ムーディ線図は、層流と乱流の異なる流動領域を示し、管の粗さやレイノルズ数の変化に伴う摩擦係数の変化を表現します。
特に、相対粗さが異なる場合の流体挙動を理解するのに役立ちます。
CAEにおける重要性
CAE(Computer-Aided Engineering)の分野では、ムーディ線図は流体シミュレーションや圧力損失の解析に広く用いられます。
流体シミュレーションを行う際、管内の圧力損失や摩擦係数を正確に求める必要があり、ムーディ線図を使って摩擦係数を得ることができます。
例えば、HVACシステムの設計や、石油・ガスパイプラインの圧力損失解析などでは、流体の速度や管の表面粗さが設計上の重要な要素です。
CAEツールにムーディ線図のデータを組み込むことで、現実に近い流れのシミュレーションを効率よく行うことができます。
これにより、設計の最適化やコスト削減が可能となります。
物理的意味合い
ムーディ線図は、物理的に見ると、管内の流れがどのように抵抗を受け、どれだけのエネルギーを消費するかを示しています。
具体的には、以下の要素が物理的に重要です。
- レイノルズ数は、流れが層流か乱流かを示す無次元数で、低いレイノルズ数では層流、高いレイノルズ数では乱流となります。
層流では流れが整然と進むのに対し、乱流ではエネルギーが渦や摩擦で失われやすくなります。 - 相対粗さは、管内壁の粗さと管径の比であり、管が滑らかであればエネルギー損失は少なく、粗い場合は摩擦損失が大きくなります。
これは乱流領域で特に顕著に現れます。 - 摩擦係数(\( f \) )は、流れが管内で受ける抵抗を表す指標で、ムーディ線図を使ってレイノルズ数と相対粗さに基づいて算出されます。
この線図を活用することで、エネルギー効率の良い配管設計が可能になり、エンジニアは流体システムにおけるコスト削減や性能向上を実現できます。
まとめ
ムーディ線図は、流体力学の分野で管内流れの圧力損失を計算する際に非常に有用なツールです。
層流と乱流の両方の領域で摩擦係数を視覚的に理解できるため、流体の挙動を簡単に予測することができます。
特にCAEでは、ムーディ線図を用いることで、より正確な流体シミュレーションが可能になり、配管設計や圧力損失解析において重要な役割を果たします。
ムーディ線図の理解と活用により、エンジニアは効率的で高性能な流体システムを設計することができます。ぜひ、実際の設計や解析に役立ててください。




コメント