配管システムにおいて、圧力損失は非常に重要な要素です。
配管内を流れる流体は、摩擦や配管の形状などの影響を受け、エネルギーを失います。
このエネルギーの損失が「圧力損失」と呼ばれるものです。
圧力損失を正確に計算することは、システム全体の効率や安全性を確保するために不可欠です。
適切な圧力を維持するために、配管の設計者は圧力損失を事前に予測し、それに基づいてシステムを最適化する必要があります。
このブログ記事では、圧力損失の基本的な概念から、直管部の圧力損失の計算方法までを詳しく解説します。
特に、ダルシー・ワイズバッハの式を中心に、レイノルズ数の計算や、層流と乱流における管摩擦係数の求め方についても触れます。
圧力損失とは
圧力損失とは、流体が配管を通過する際に、そのエネルギーの一部が摩擦や乱流などによって失われる現象を指します。
これにより、流体の流れに必要な圧力が低下し、システム全体の効率が損なわれる可能性があります。
圧力損失を正確に理解し、計算することは、配管設計や流体輸送システムにおいて極めて重要です。
圧力損失の原因
圧力損失の主な原因は、配管内の流体が配管の内壁や曲がり部分と接触することによって発生する摩擦です。
この摩擦は、配管の長さや内径、流体の速度や粘度、さらには配管内壁の粗さなどによって影響を受けます。
また、配管内の流れが直線的でない場合(例えば、曲がり管や分岐管を通過する場合)、さらに大きな圧力損失が発生します。
圧力損失の影響
圧力損失が大きいと、流体を所定の速度で運ぶために必要な圧力が増加し、ポンプやコンプレッサーの負荷が高まります。
その結果、エネルギーコストが増大し、システム全体の効率が低下します。
また、過剰な圧力損失は、機器や配管の故障リスクを高める原因にもなり得ます。
圧力損失の計算の重要性
圧力損失を事前に正確に計算することで、適切な配管設計が可能になります。
これにより、必要なポンプ容量の決定や、エネルギー効率の最適化、システムの信頼性向上が実現できます。
配管設計者やエンジニアにとって、圧力損失の計算は日常的な業務の一部であり、システム全体のパフォーマンスを左右する重要な要素です。
圧力損失の計算方法:ダルシー・ワイズバッハの式
配管内の圧力損失を計算するために、最も広く用いられているのが「ダルシー・ワイズバッハの式」です。
この式は、流体の流れによる摩擦損失を定量的に表現するもので、配管設計や流体力学の分野で非常に重要な役割を果たしています。
この章では、ダルシー・ワイズバッハの式の概要と、圧力損失を計算する際に必要な各パラメータについて説明します。
ダルシー・ワイズバッハの式とは
ダルシー・ワイズバッハの式は、以下のように表されます。
$$
h_f = \lambda \cdot \frac{L}{D} \cdot \frac{v^2}{2g}
$$
ここで、各記号の意味は次の通りです。
- \( h_f \) :圧力損失(m)
- \( \lambda \) :管摩擦係数(無次元)
- \( L \) :配管の長さ(m)
- \( D \) :配管の内径(m)
- \( v \) :管内の流速(m/s)
- \( g \) :重力加速度(m/s²)
この式は、流体が配管内を流れる際に発生する摩擦による圧力損失を示しています。
式の各項目は、配管設計において重要なパラメータであり、それぞれが圧力損失に大きな影響を与えます。
ダルシー・ワイズバッハの式の構成要素
- 圧力損失 \( h_f \) :配管内で失われる圧力を表します。この値が大きいほど、ポンプや他の機械的装置が追加のエネルギーを必要とします。
- 管摩擦係数 \( \lambda \) :摩擦の影響を表す無次元数で、後の章で詳しく説明しますが、層流や乱流の状態によって異なります。
- 配管の長さ \( L \) :流体が移動する距離を表します。配管が長くなるほど、圧力損失は増加します。
- 配管の内径 \( D \) :配管の太さを表します。配管の内径が大きいほど、流体の接触面積が減少し、圧力損失が小さくなります。
- 流速 \( v \) :流体の速度を表します。流速が速いほど、圧力損失は大きくなります。
圧力損失計算の全体的な流れ
直管部の圧力損失を計算する際の手順は、次のようになります。
- レイノルズ数を算出し、流れの状態(層流か乱流か)を判断します。
- 流れの状態に応じて、管摩擦係数λを算出します。
- ダルシー・ワイズバッハの式を使用して、圧力損失を求めます。
次の章では、まずレイノルズ数の計算方法と、流れの分類について詳しく解説していきます。
レイノルズ数と流れの分類
配管内を流れる流体の状態を理解するために、まず「レイノルズ数( \( Re \) )」を計算することが重要です。
レイノルズ数は、流体の流れが層流か乱流かを判断するための無次元数です。
流体の流れの種類を判別することで、圧力損失を正確に計算するために必要な管摩擦係数( \( \lambda \) )を適切に選ぶことができます。
レイノルズ数とは
レイノルズ数は、以下の式で表されます。
$$
Re = \frac{\rho \cdot v \cdot D}{\mu}
$$
ここで、各記号の意味は次の通りです。
- \( Re \) :レイノルズ数(無次元)
- \( \rho \) :流体の密度(kg/m³)
- \( v \) :流体の流速(m/s)
- \( D \) :配管の内径(m)
- \( \mu \) :流体の動粘度(Pa・s)
レイノルズ数は、流体の慣性力と粘性力の比を表し、その値により流れの状態が決まります。
流れの分類
レイノルズ数に基づき、流れは以下の3つの状態に分類されます。
- 層流(Laminar Flow):
- \( Re < 2100 \) の場合、流れは層流です。層流では、流体は配管内を滑らかに、層をなして流れます。この場合、流体の層が互いにすべらずに規則正しく流れるため、摩擦損失が少なくなります。
- 乱流(Turbulent Flow):
- \( Re > 4000 \) の場合、流れは乱流です。乱流では、流体は不規則に混ざり合い、渦を巻きながら流れます。これにより、摩擦が増加し、圧力損失も大きくなります。
- 遷移流(Transitional Flow):
- \( 2100 < Re < 4000 \) の場合、流れは遷移流と呼ばれる状態で、層流と乱流が混在します。この範囲では流れの性質が不安定で、どちらの状態にも移行する可能性があります。
- 実際の設計においては、遷移流は扱いにくく、この範囲内では乱流として扱うことが多いです。
レイノルズ数の計算例
具体的な例として、内径50 mmの配管内を水(密度 = 1000 kg/m³、動粘度 = 1.0×10⁻³ Pa・s)が2 m/sの速度で流れる場合のレイノルズ数を計算してみましょう。
$$
Re = \frac{1000 \cdot 2 \cdot 0.05}{1.0 \times 10^{-3}} = 100,000
$$
この結果、レイノルズ数が100,000となり、これは【 乱流 】であることを示しています。
次に、このレイノルズ数に基づいて、層流と乱流のそれぞれの場合における管摩擦係数( \( \lambda \) )の求め方について説明します。
管摩擦係数 \( \lambda \) の算出方法
レイノルズ数によって流れの状態が層流か乱流かを判別した後、それぞれの流れに対応した管摩擦係数( \( \lambda \) )を求める必要があります。
管摩擦係数は、配管内の流体の摩擦によるエネルギー損失を表す重要なパラメータで、圧力損失の計算に直接影響を与えます。
層流の場合の管摩擦係数 \( \lambda \)
層流の状態では、流体が配管内を規則正しく層をなして流れるため、摩擦損失は比較的小さくなります。
この場合の管摩擦係数 \( \lambda \) は、次のように簡単な式で求められます。
$$
\lambda = \frac{64}{Re}
$$
この式からわかるように、層流における管摩擦係数はレイノルズ数に反比例します。
レイノルズ数が小さい(流体がゆっくりと流れる)ほど摩擦係数は大きくなり、
逆に、レイノルズ数が大きい(流体の流れが速い)ほど摩擦係数は小さくなります。
乱流の場合の管摩擦係数 \( \lambda \)
乱流の場合、流体は配管内で不規則に混ざり合い、渦を巻くように流れるため、摩擦損失が大きくなります。
乱流における管摩擦係数を求めるためには、より複雑な式が必要です。
実用的には、次の「コールブルック・ホワイトの式」が広く使用されています。
$$
\frac{1}{\sqrt{\lambda}} = -2.0 \log\left( \frac{ks/D}{3.7} + \frac{2.51}{Re \sqrt{\lambda}} \right)
$$
ここで、
- \( ks \) :配管内の等価砂粒径(m)
- \( D \) :配管の内径(m)
- \( Re \) :レイノルズ数(無次元)
- \( \lambda \) :管摩擦係数(無次元)
この式は、配管の内壁が粗い(壁面に凸凹がある場合)の摩擦係数を考慮しています。
計算は複雑ですが、現代では数値解法や計算ツールを用いて簡単に求めることが可能です。
ムーディ線図の利用
管摩擦係数 \( λ \) を簡単に求めるために、「ムーディ線図」を使用することが一般的です。
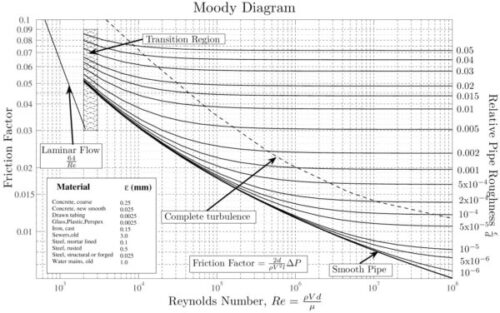
ムーディ線図は、縦軸に管摩擦係数 \( λ \) 、横軸にレイノルズ数 \( Re \) をとったグラフで、
層流と乱流の両方の領域をカバーしています。
この図を使用することで、レイノルズ数と配管の粗さに基づいて、容易に管摩擦係数を見積もることができます。
例えば、配管の内壁が滑らかな場合や粗い場合、それぞれの条件に応じた曲線を使用して \( λ \) を読み取ります。
この方法は、特に乱流の計算で便利であり、設計者が直感的に摩擦係数を把握するために広く利用されています。
まとめ
配管システムにおける圧力損失は、流体が配管を通過する際にエネルギーが失われる現象であり、配管の設計やシステムの効率性に直接影響を及ぼします。
圧力損失の計算は、適切な配管設計を行い、エネルギー効率を最適化し、システムの信頼性を高めるために不可欠です。
圧力損失の主な原因は、流体が配管の内壁や曲がり部分で発生する摩擦です。
これにより、ポンプやコンプレッサーにかかる負荷が増し、エネルギーコストが上昇する可能性があります。
圧力損失の正確な計算には、ダルシー・ワイズバッハの式が広く用いられ、流体の状態に応じた管摩擦係数の求め方も重要です。
レイノルズ数の計算によって流れの状態(層流、乱流、遷移流)を把握し、それに基づいて管摩擦係数を求めることで、圧力損失の正確な予測が可能になります。
これにより、設計者はより効率的な配管システムを構築することができ、システムのパフォーマンスを最適化できます。
次回は曲がり管やバルブなどの要素を加味した、より現実的な計算をご紹介します。お楽しみにしてください!







コメント