サマリ
数値流体力学(CFD)を用いて円柱周りに発生するカルマン渦を再現し、理論値との比較を行います。
円柱流れとカルマン渦とは
円柱流れとは、一様な流れの中に円柱を置いた場合に、円柱の後流に発生する渦のことを指します。
特に、流れが円柱に衝突し、物体からはく離する際に生じる渦は、レイノルズ数によって性質が変化します。
レイノルズ数が小さい場合、渦は対称的になりますが、レイノルズ数がある程度大きくなると、非対称なカルマン渦が発生します。
今回のサンプルでは、CFDを用いて円柱周りの流れをシミュレートし、カルマン渦を再現。その結果を理論的な予測値と比較することを目的としています。
ストローハル数とは
流体力学において、ストローハル数( \( \text{St} \) )は非常に重要な無次元数です。
これは、物体から発生する渦の放出周波数 ( \( f \) ) を、物体の代表長さ(円柱の場合は直径 ( \( d \) ) )および主流の速度 ( \( U \) ) で無次元化したものです。
$$
\text{St} = \frac{f \cdot d}{U}
$$
このストローハル数は、流れにおける振動現象の周波数を示し、特に円柱の場合、広いレイノルズ数範囲(200~2×10^5)で約0.2という値を取ります。
解析結果
以下の図は、シミュレーションの結果として得られたカルマン渦の発生を示しています。
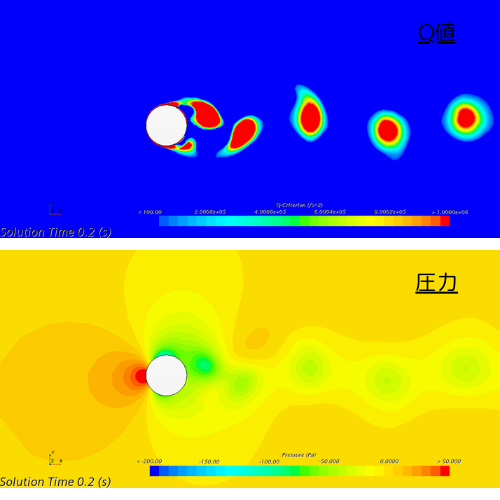
- 上図 : Q値のコンター図。この図から、非対称なカルマン渦が発生していることが確認できます。
- 下図 : 圧力のコンター図。渦が存在する領域では圧力が低いことが分かります。
また、揚力の時間履歴を確認すると、周期的な波形を示しています。
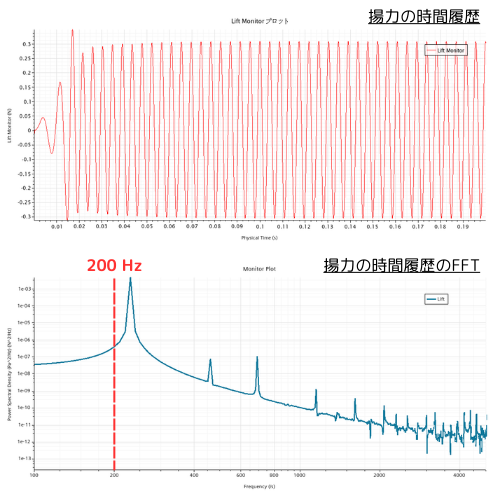
この波形に対してFFT(高速フーリエ変換)を適用することで、渦列の周波数を求めます。
円柱の直径が0.01 m、流速が10 m/sの場合、ストローハル数が0.2であれば、周波数は以下のように計算されます。
$$
f = \frac{0.2 \cdot U}{d} = 200 \text{ Hz}
$$
今回は2次元モデルを使用しているため、実際の周波数は200 Hzに完全には一致しませんが、非常に近い値を示します。
まとめ
このサンプルを通じて、数値流体力学を用いたカルマン渦の再現と、理論的なストローハル数との比較を行いました。CFDの活用により、流体力学の理論と現象の理解がさらに深まることを期待します。






コメント