ダーシーの法則
一言で表すと、、
ダーシーの法則とは、多孔質媒体内を流れる流体の速度が、圧力勾配に比例することを示す基本的な流体力学の法則です。
概要
ダーシーの法則は、19世紀のフランスの技師アンリ・ダーシー(Henry Darcy)によって導き出され、多孔質媒体を通じて流れる流体の挙動を記述するための基本的な法則です。地下水の流動や石油工学、環境工学など、さまざまな分野で広く利用されています。
この法則は、流体が多孔質材料を通過する際の流れの特性を定量化するのに不可欠であり、エンジニアリングやシミュレーションにおいても重要な役割を果たします。
イメージ
ダーシーの法則をイメージするための簡単な例として、砂の層に水を注ぐシーンを考えてみましょう。水は砂の層を通って下方に流れます。このとき、水の流速は、砂の層の厚み(つまり、流れる距離)と水の圧力差によって決まります。ダーシーの法則は、この流速と圧力差の関係を数式で表しています。
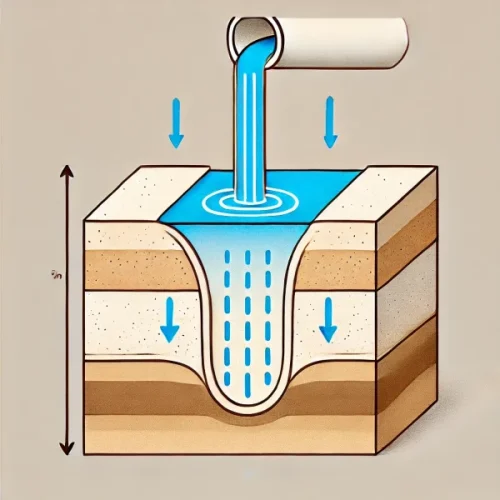
例えば、フィルターにおける水の浸透速度や、地下水が地中を移動する速度を計算する際に、この法則が用いられます。
定義
ダーシーの法則は、次のように定義されます:
$$
Q = -\frac{K A \Delta P}{\mu L}
$$
ここで、
- \( Q \) : 流量(単位時間あたりの流体の体積)
- \( K \) : 浸透率(Permeability)— ポーラスメディアの透水性を示す定数
- \( A \) : 流れが通過する断面積
- \( \Delta P \) : 流体が流れる方向の圧力差
- \( \mu \) : 流体の粘度
- \( L \) : 流れの方向に沿ったポーラスメディアの長さ
また、流速 \( U \) を求める場合には次のように表せます:
$$
U = -\frac{K \Delta P}{\mu L}
$$
ダーシーの法則の中で重要なのは、流体の速度が圧力勾配に比例することです。この法則は、流体が比較的低速で流れる場合に適用され、粘性支配的な流れを対象としています。
高速度領域では、慣性効果が無視できなくなるため、ダーシーの法則は修正が必要です(たとえば、Forchheimerの拡張が考慮される場合があります)。
CAEにおける重要性
計算機支援工学(CAE)において、ダーシーの法則は多孔質媒体内の流体の動きをシミュレーションする際の基礎となります。地下水流動解析、石油リザーバーシミュレーション、フィルター設計など、多くの分野でこの法則を利用して、流体の動きや圧力損失を予測します。
例えば、石油工学では、地下の多孔質岩層を通過する原油の移動を解析する際にダーシーの法則を用います。これにより、最適な採掘方法を計画したり、リザーバーの寿命を予測したりすることが可能です。また、環境工学においては、地下水の汚染物質の拡散や浄化プロセスのシミュレーションにも用いられます。
物理的意味合い
ダーシーの法則は、ポーラスメディア内の流体挙動を理解するために不可欠な物理的意味合いを持っています。具体的には、以下の点が挙げられます:
- 浸透率( \( K \) ): ポーラスメディアの浸透率は、その材料がどれだけ流体を通しやすいかを示す指標です。浸透率が高いほど、流体は容易に通過します。
- 圧力勾配( \( \Delta P \) ): 流体を流すためには、一定の圧力差が必要です。圧力勾配が大きいほど、流速も速くなります。
- 粘性( \( \mu \) ): 流体の粘性は、流体が流れる際の内部抵抗を表します。粘性が高いほど、流体は流れにくくなります。
これらの物理的パラメータがどのように流れに影響を与えるかを理解することで、流体力学における現象の解析や制御が可能となります。
まとめ
ダーシーの法則は、多孔質媒体内の流体の流れを理解するための基本的な理論です。浸透率や圧力勾配、流体の粘性といった要素が流速にどのように影響するかを定量的に示しており、これにより多くの実際の問題に応用することができます。流体力学やエンジニアリング、環境科学において、この法則の理解は、より高度な設計や解析を行うための重要なステップとなります。



コメント