クーラン数
一言で表すと、、
クーラン数とは、数値解析において解の安定性を左右する重要なパラメータです。
概要
クーラン数(Courant Number)は、数値解析における時間ステップの選定や計算の安定性に大きく関わる指標です。
特に、流体力学や熱伝導解析などの分野で頻繁に登場し、解が収束するかどうかを判断するための基準となります。
クーラン数が適切でない場合、シミュレーション結果が発散するリスクが高まり、解析精度に悪影響を及ぼす可能性があります。
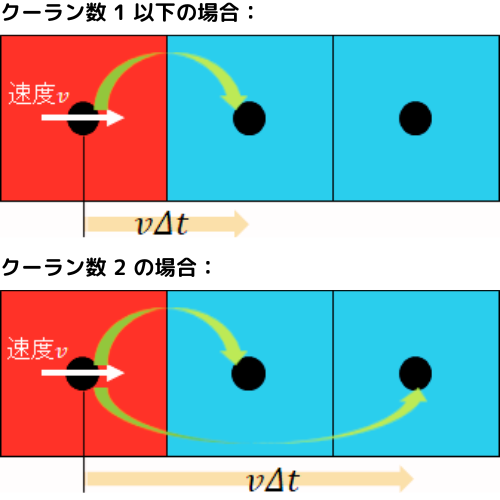
イメージ
クーラン数は、波や情報が計算グリッドをどの程度進むかを表すものと考えられます。
例えば、クーラン数が1に近い場合、波は1つの時間ステップでちょうど1つの計算セルを進むイメージです。
クーラン数が大きすぎると、情報が一度に複数のセルを飛び越えてしまい、解の不安定性を引き起こします。
定義
クーラン数 \( C \) は、次の式で定義されます。
$$
C = \frac{v \cdot \Delta t}{\Delta x}
$$
ここで、
- \( v \) : 波や流れの速度
- \( \Delta t \) : 時間ステップ
- \( \Delta x \) : 空間グリッドの幅
この定義から、クーラン数は「ある時間ステップにおける情報の移動距離と、グリッド間隔の比率」であることがわかります。
CAEにおける重要性
CAE(Computer-Aided Engineering)解析において、クーラン数は特に重要な役割を果たします。適切なクーラン数を設定することで、数値解析の安定性が確保され、正確な結果を得ることが可能です。例えば、流体解析では、クーラン数が1以下であることがしばしば求められます。これにより、時間ステップが適切に設定され、物理的に妥当な結果が得られる確率が高まります。
物理的意味合い
クーラン数が示す物理的意味は、「時間ステップ内で情報がどれだけ伝播するか」ということです。
クーラン数が1を超えると、情報が計算セルを飛び越えてしまい、物理現象を正確に捉えることが難しくなります。
一方、クーラン数が1以下であれば、情報が順序正しく伝わり、解析結果の信頼性が向上します。
したがって、数値シミュレーションにおいて、クーラン数の適切な設定は欠かせません。
まとめ
クーラン数は数値解析、特にCAE解析における重要な指標であり、その適切な設定が解析結果の精度や安定性に直結します。
クーラン数が適切でないと、シミュレーションが発散するリスクが高まり、信頼性が低下する可能性があります。
したがって、解析の目的や物理現象に応じて、クーラン数を慎重に選定することが求められます。





コメント