永田の式は、撹拌翼や撹拌槽の設計において、動力数 \( N_P \) を求めるために使われる重要な公式です。
この動力数を正確に算出することで、撹拌装置の効率や性能を最適化できます。
この記事では、撹拌翼の枚数や段数を考慮して修正された永田の式に基づく動力数を、簡単に計算できるオンラインツールを紹介します。
永田の式とは
永田の式は以下のように表されます:
$$
N_P = \frac{A}{Re} + B \left( \frac{10^3 + 1.2Re^{0.66}}{10^3 + 3.2Re^{0.66}} \right)^p \left( \frac{H}{D} \right)^{(0.35 + b’/D)}
$$
ここで、撹拌翼の修正された翼幅 \( b’ \) は次の式で計算されます:
$$
b’ = \frac{n_p}{2} \times b \times N
$$
各パラメータは次の通りです:
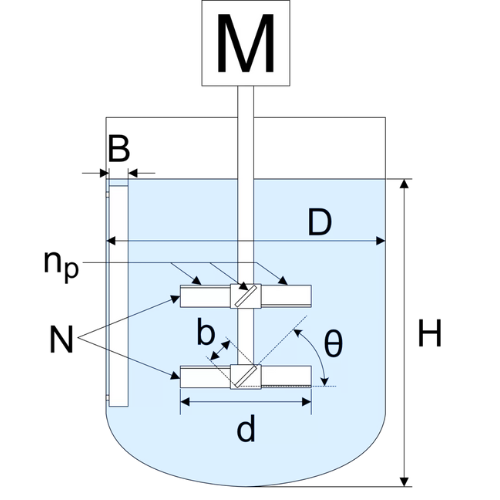
- \( N_P \) : 動力数(無次元)
- \( Re \) : レイノルズ数(無次元)
- \( H \) : 液深さ(m)
- \( D \) : 撹拌槽の直径(m)
- \( b \) : 撹拌翼の幅(m)
- \( d \) : 撹拌翼の直径(m)
- \( n_p \) : 撹拌翼の枚数(無次元)
- \( N \) : 翼の段数(無次元)
この公式により、撹拌槽や翼の設計における動力数を算出し、効率的な撹拌装置の開発に貢献します。
永田の式(動力数)計算ツール
以下のツールを使えば、永田の式に基づいて動力数を簡単に計算できます。
撹拌槽や撹拌翼の設計を効率化するために、ぜひご活用ください!
2枚羽根1段翼の場合
永田の式は翼幅と液深さの比(b’/H)が1を超えない範囲で利用できます。
動力数 \( N_P \):
2枚羽根1段翼とは異なる場合
永田の式は羽根枚数 \( n_p = 2 \)、翼の段数 \( N = 1 \) での推算式です。
羽根枚数が違ったり多段翼の場合は、厚みのある2枚羽根1段パドル翼と仮定し、修正して用います。
動力数 \( N_P \):
活用シーン
このツールは、撹拌槽設計や数値解析を行う際に役立ちます。
撹拌装置の動力数を簡単に求め、設計を効率化するためにご利用ください。
- 撹拌装置の設計
- 撹拌槽の数値解析
- 工学シミュレーション
まとめ
永田の式を用いた動力数の計算は、撹拌装置の性能評価に欠かせません。
このツールを使用すれば、撹拌翼の枚数や段数を考慮して、簡単に計算結果を得ることができます。
撹拌槽設計の効率化にぜひお役立てください!




コメント