概要
配管内の圧力損失計算に使用される式がファニングの式です。
流体が配管を流れる際、摩擦によって圧力が低下し、その圧力損失は次のように計算されます。
$$
\Delta P = 4f \frac{\rho u^2}{2} \frac{L}{d}
$$
- \( \Delta P \) : 圧力損失 [Pa]
- \( f \) : 摩擦係数 [-]
- \( \rho \) : 流体密度 [kg/m³]
- \( u \) : 流体の平均速度 [m/s]
- \( L \) : 配管の長さ [m]
- \( d \) : 配管の直径 [m]
ファニングの式は、ポンプの揚程計算において、直管で発生する圧力損失を算出するために使われます。
この計算により、流体が目的の場所まで効率よく運ばれるためのポンプ性能を見積もることができます。
圧力損失と揚程計算
以前の記事で解説した【ベルヌーイの定理】において、摩擦損失水頭( \( h_f \) )が登場しました。
この \( h_f \) は、ファニングの式で求めた圧力損失 ( \( \Delta P \) ) を次の式で変換することによって計算されます。
$$
h_f = \frac{\Delta P}{\rho g}
$$
この変換によって、圧力単位 [Pa] で求めた損失を、水頭(高さ)の単位に変換できます。
これにより、配管内の摩擦によるエネルギー損失がポンプの揚程計算に適用されるようになります。
もしファニングの式で圧力損失を無視した場合、摩擦によるエネルギー損失が考慮されないため、流体を目的の場所まで運ぶことができません。
したがって、圧力損失を正確に計算し、それに基づいてポンプの揚程を決定することが重要です。
ファニングの式の導出
ファニングの式は、配管内を流れる流体の摩擦力と圧力損失の関係から導出されます。
流体が配管壁面に及ぼす摩擦力
流体が配管内を平均流速 \( u \) で流れていると仮定します。
このとき、流体の粘性により壁面に摩擦力 \( F \) が働きます。この力は次の式で表されます。
$$
F = f \cdot \left( \pi d L \right) \cdot \frac{1}{2} \rho u^2
$$
ここで、摩擦係数 \( f \) は配管の表面粗さや流体の流れの状態に依存します。
圧力降下による力の損失
配管の長さ \( L \) の区間における圧力降下によって発生する力の損失 \( F_L \) は、次の式で表されます。
$$
F_L = \frac{\pi d^2}{4} \left( P_1 – P_2 \right) = \frac{\pi d^2}{4} \Delta P
$$
ファニングの式の導出
流体が壁面に及ぼす摩擦力 \( F \) と、この区間での圧力降下による力の損失 \( F_L \) が等しいと仮定すると、次のようになります。
$$
f \cdot (\pi d L) \cdot \frac{1}{2} \rho u^2 = \frac{\pi d^2}{4} \Delta P
$$
これを整理すると、ファニングの式が導かれます。
$$
\Delta P = 4f \frac{\rho u^2}{2} \frac{L}{d}
$$
摩擦係数 \( f \) の使い分け
摩擦係数 \( f \) は、流体の流れの状態や配管の壁面の粗さによって変わるため、適切に値を選定することが重要です。
流体の状態によって、次のような異なる式を使用します。
- 層流( \( Re \leq 2,000 \) ):
$$
f = \frac{16}{Re}
$$ - 乱流( \( 3,000 \leq Re \leq 100,000 \) ):
$$
f = 0.0791 Re^{-0.25}
$$
また、ムーディ線図を使用して、さまざまな実験結果に基づいた摩擦係数 \( f \) を読み取る方法もあります。
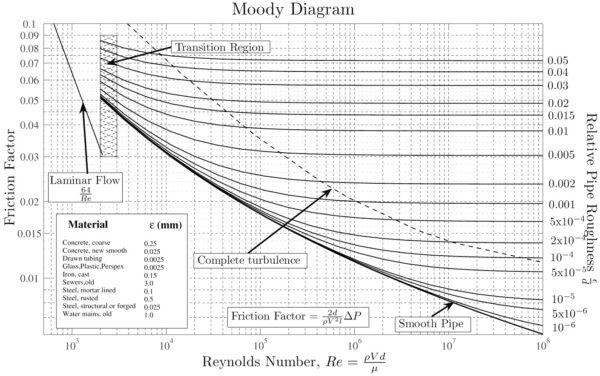
ムーディ線図は、機械工学で広く使われ、摩擦係数 \( f \) ではなく\( \lambda \) が縦軸にプロットされていることが多いです。
ダルシー・ワイズバッハの式との関係
機械工学の分野では、ファニングの式と似た意味を持つダルシー・ワイズバッハの式が使用されます。
この式は次のように表されます。
$$
h_f = \frac{\Delta P}{\rho g} = \lambda \frac{u^2}{2g} \frac{L}{d}
$$
ここで \( \lambda \) はダルシー摩擦係数です。
ファニングの式を摩擦損失水頭 \( h_f \) の式に代入すると、次のように表されます。
$$
h_f = 4f \frac{u^2}{2g} \frac{L}{d}
$$
2つの式を比較すると、次の関係が成り立ちます。
$$
\lambda = 4f
$$
したがって、ムーディ線図で読み取った \( \lambda \) を 4 で割ることで摩擦係数 \( f \) が得られます。
計算時には、この変換を忘れずに行いましょう。
まとめ
ファニングの式は、配管内の圧力損失を計算するための重要なツールです。
流体が配管を流れる際、摩擦によりエネルギーが失われ、ポンプの揚程計算にも影響を与えます。
この圧力損失を正確に見積もることで、流体を効率よく目的の場所まで送るためのポンプ性能を最適化できます。
また、摩擦係数 \( f \) の正確な算出は、流れの状態や配管の壁面状態に依存します。
実務では、ムーディ線図や層流・乱流の公式を活用して、正しい摩擦係数を使用することが求められます。
さらに、ダルシー・ワイズバッハの式との関係も理解し、正確な圧力損失計算に役立てましょう。





コメント